反距离权重（IDW）和克里金（Kriging）的比较与应用

本文在我的博客同步发布和更新。

在地理数据科学领域，追求完美无瑕的数据似乎总是难以实现。现实中，数据缺失、分辨率粗糙、采样不均是普遍现象，而这些问题对分析和可视化有着显著的影响。如何修复这些数据缺陷？空间插值或许是你的答案。

什么是空间插值？

插值是一种数学方法，用于估计已知数据点之间的值。空间插值特别强调地理位置的影响，通过距离来判断未知点的可能属性。

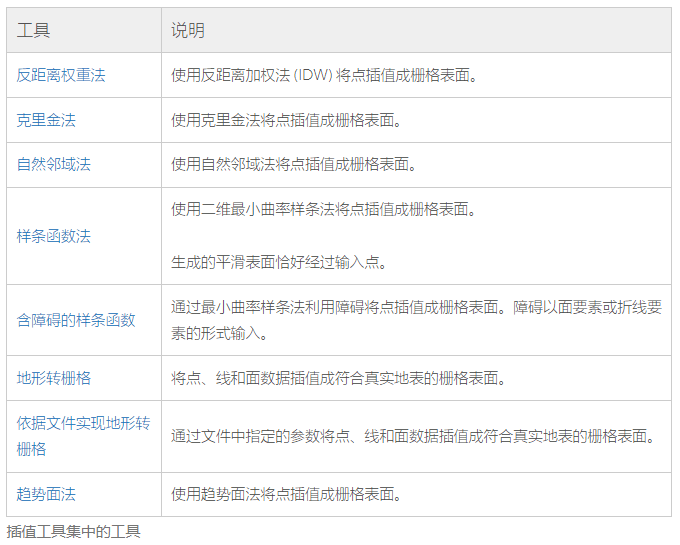
反距离权重（IDW）和克里金（Kriging）是两种最常用的空间插值方法，各有优劣，适用于不同的场景。

反距离权重（IDW）

反距离权重 是一种直观、易于理解的插值方法。基本理念就是—越接近的点越相似。这很符合托布勒第一地理定律：“一切事物都相互关联，但近的事物比远的更相关。”反距离权重通过距离给每个已知点分配权重，距离越近，权重越大。

优点：

• 简单易懂：适合快速分析，便于初学者使用。
• 计算高效：特别适合中小型数据集。
• 平滑过渡：产生的表面平滑，适合地形建模。

局限性：

• 对异常值敏感：邻近点影响大，可能导致异常值对结果的过度影响。
• 缺乏结构信息：无法捕捉复杂的空间模式。

克里金（Kriging）

克里金是一种更为复杂的插值方法，考虑了数据间的空间相关性，能结合局部变化和整体趋势。它不仅能预测值，还能提供不确定性的评估。

优点：

• 空间高效：适用于复杂空间结构的数据。
• 不确定性评估：有助于了解结果的可靠性。
• 优化估计：通过变异函数模型调整权重，降低误差。

局限性：

• 计算开销大：需要求解大型方程组，对计算资源要求高。
• 模型选择复杂：合适的变异函数模型至关重要，选错可能导致不准确的结果。
• 依赖统计假设：当假设不成立时，可能无法提供最佳预测。

反距离权重 与克里金：如何选择？

选择 反距离权重 还是克里金，取决于数据特性和分析目标。如果你的数据简单且需要快速处理，IDW 可能是更好的选择。而如果数据具有复杂的空间结构，且你希望精确预测并量化不确定性，克里金则是更好的选择。

实例分析

以美国亚利桑那州科科尼诺县（地形复杂多样，包含了广袤的高原、深峡谷和森林。）的高度为例，我们对数据进行插值处理。随机移除 20%的数据后，用 IDW 和克里金方法分别进行插值，结果显示克里金的预测误差更低。

红色为随机移除的 h3 单元

插值结果

我们可以在地图上看到插值结果，上层为反距离权重，下层为克里金。结果的误差分布如下图所示：

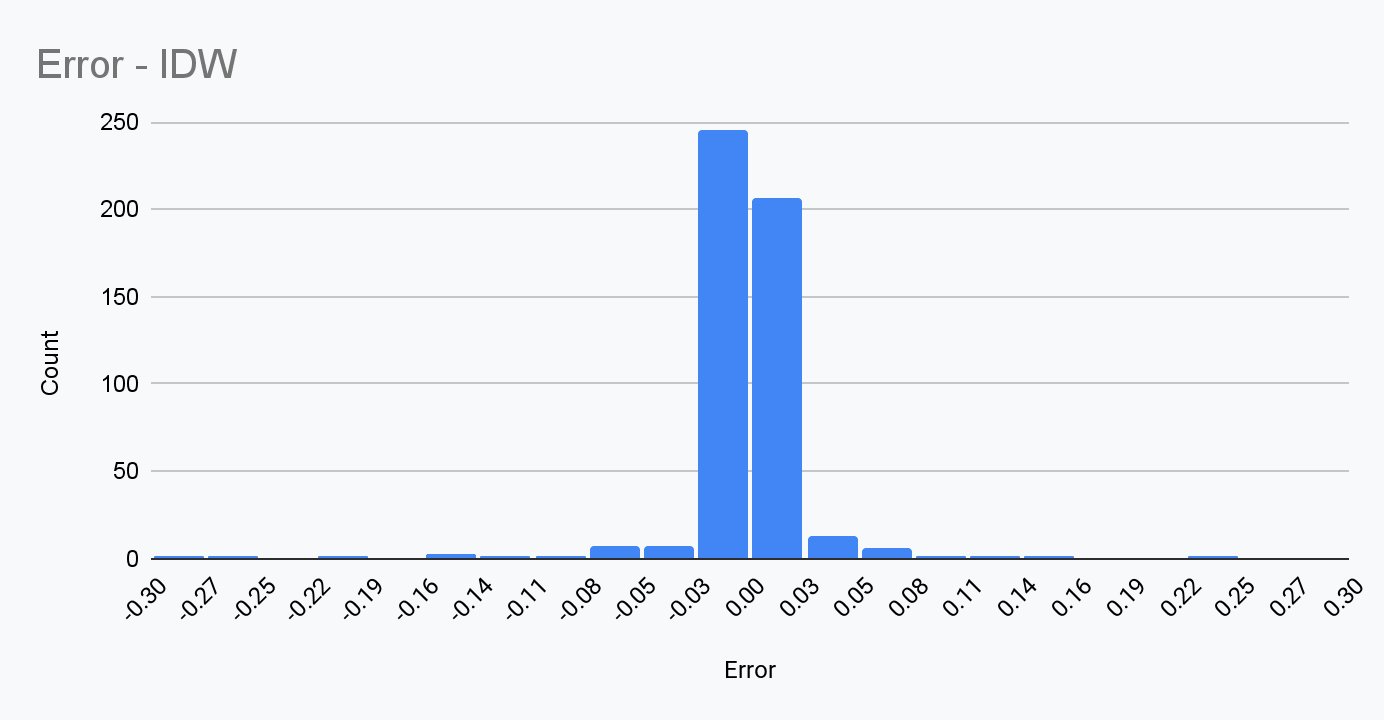
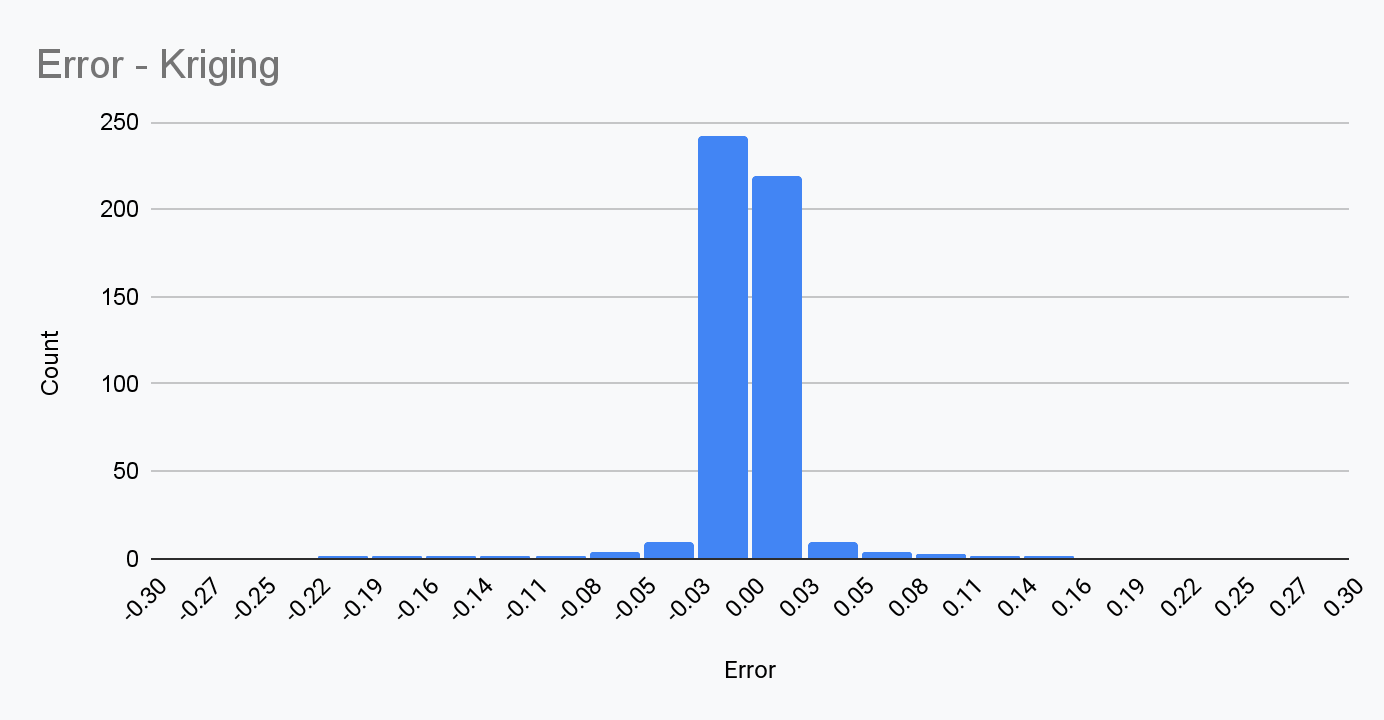
结果如下：

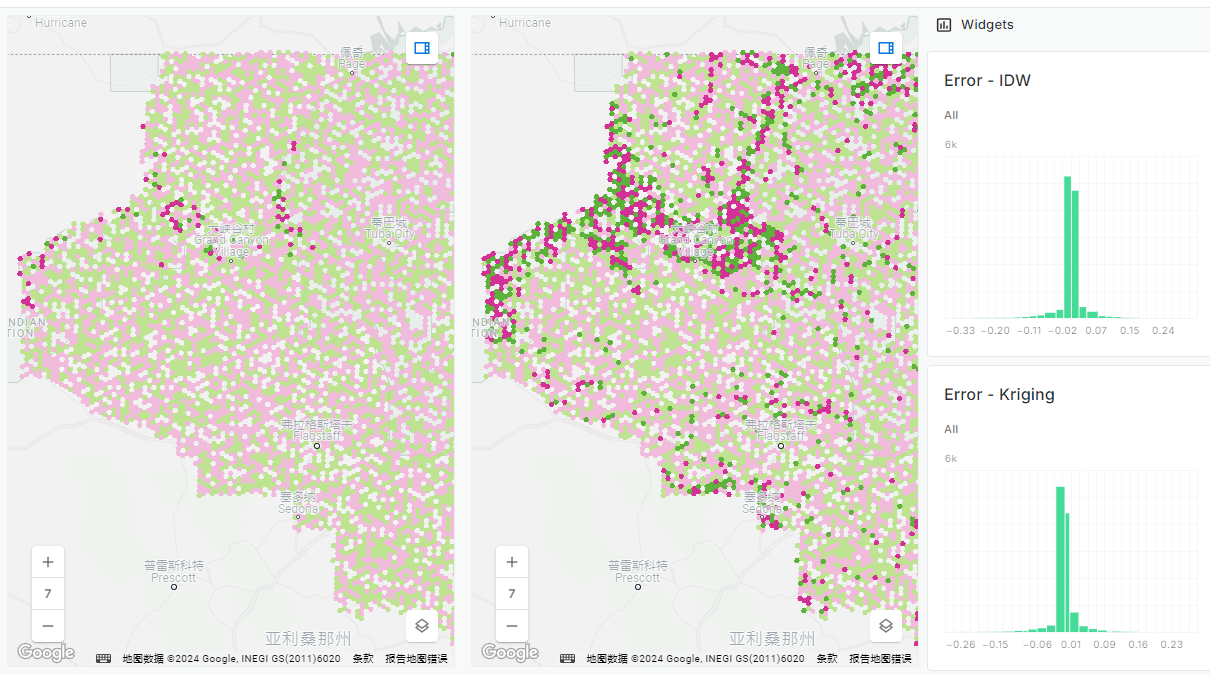
但并不是所有情况下克里金都优于 反距离权重，这要取决于数据的空间特征。

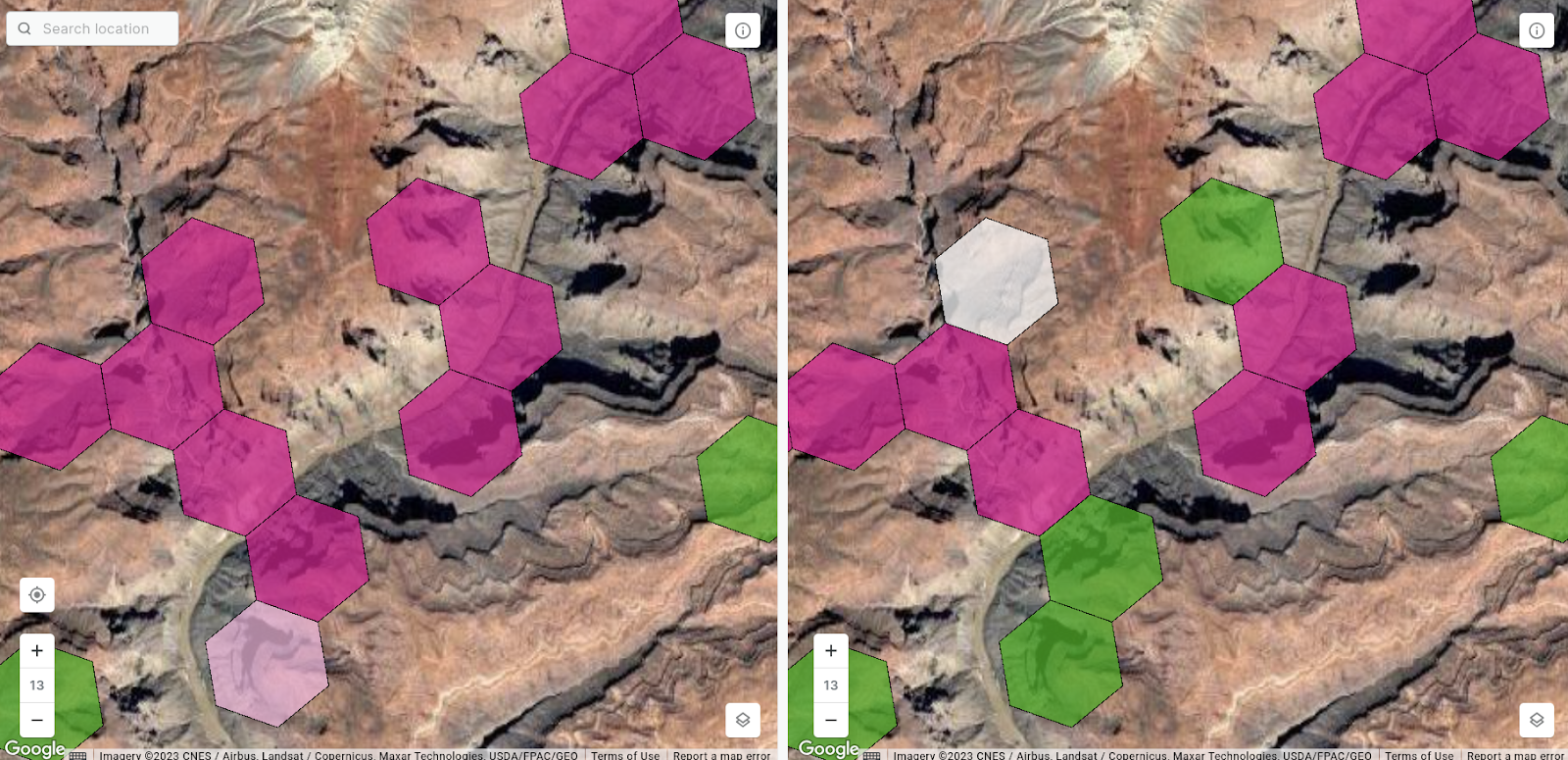
H3 单元也过于粗糙，无法准确预测如此局部的地形变化，使用更详细的地形模型（比如点图层）可能会产生更准确的结果。

插值的核心原则是：理解地理特性。

无论采用哪种方法，理解数据的空间特性至关重要。在地形复杂的地方，比如大峡谷，精细的模型往往能得到更好的结果。所以，插值的成功关键在于：理解地理特征，明确目标模式，调整分析方法。

文中美国亚利桑那州科科尼诺县的实例来自：# Spatial interpolation: which technique is best & how to run it